
















Մնացորդով բաժանում

Ախոռում կա \(14\) ձի: Դրանցից կազմեցին \(2\) ձիով լծված կառքեր:
Քանի՞ կառք ստացվեց:
Ստացվեց կառք:
Հաջորդ անգամ նույն \(14\) ձիերից կազմեցին \(3\) ձիով լծված կառքեր:
Քանի՞ կառք ստացվեց այս անգամ:
Ստացվեց \(4\) կառք, և \(2\) ձիեր ավելացան և մնացին ախոռում:
Դա գրում են այսպես՝
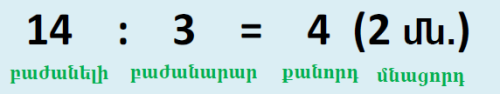
Իրոք, եթե \(4\) կառքերից յուրսքանչյուրում լծեցին \(3\)-ական ձի և ևս \(2\) ձի ավելացավ, ապա ախոռում կար \(14\) ձի՝
Անմնացորդ բաժանման ժամանակ մնացորդը հավասար է զրոյի:
Մնացորդով բաժանումը այնպիսի բաժանում է, երբ մնացորդը հավասար չէ զրոյի:
Մնացորդով բաժանման ժամանակ քանորդը անվանում են նաև թերի քանորդ:
Օրինակ
Համոզվենք, որ :
Լուծման քայլերը:
1. Գտնում ենք \(17\)-ից փոքր ամենամեծ թիվը, որն անմնացորդ բաժանվում է \(3\)-ի:
Դա \(15\)-ն է՝
2. Բաժանելիից՝ \(17\)-ից հանում ենք \(15\)՝
\(2\)-ը մնացորդն է:
3. Համեմատում ենք մնացորդն ու բաժանարարը:

Մնացորդով բաժանման ժամանակ մնացորդը միշտ փոքր է բաժանարարից:
Ուշադրություն
Ինչպե՞ս ստուգել մնացորդով բաժանումը:
1. Թերի քանորդը պետք է բազմապատկել բաժանարարով:
2. Արդյունքին գումարել մնացորդը:
3. Ստացվածը պետք է հավասար լինի բաժանելիին:
Եթե բաժանելին փոքր է բաժանարարից, ապա քանորդը հավասար է \(0\)-ի, իսկ մնացորդը հենց բաժանելին է:
Աղբյուրները
Ս. Մկրտչյան, Ս. Իսկանդարյան, Ա. Աբրահամյան, Ռ. Սարգսյան, Մաթեմատիկա 4-րդ դասարան, Զանգակ, 2013