y=k/x ֆունկցիայի գրաֆիկը — դաս։ Հանրահաշիվ, 8-րդ դասարան.

Մենք դիտարկեցինք

y = \frac{k}{x}

ֆունկցիան $k = 1$ դեպքում: Հիմա դիտարկենք $k$ -ի դրական, $1$ -ց տարբեր դեպք, օրինակ՝ $k = 2$ -ը:

Դիտարկենք

y = \frac{2}{x}

ֆունկցիան և լրացնենք նրա արժեքների աղյուսակը:

$x$	$1$	$2$	$-1$	$-2$	$4$	$\frac{1}{2}$	$-4$	$-$ $\frac{1}{2}$
$y$	$2$	$1$	$-2$	$-1$	$\frac{1}{2}$	$4$	$-$ $\frac{1}{2}$	$-4$

Կառուցենք այս կետերը կոորդինատական հարթության վրա: Ուրվագծվում է երկու ճյուղերից բաղկացած կոր: Տանենք այն:

y = \frac{1}{x}

ֆունկցիայի գրաֆիկի պես այս կորը ևս կոչվում է հիպերբոլ:

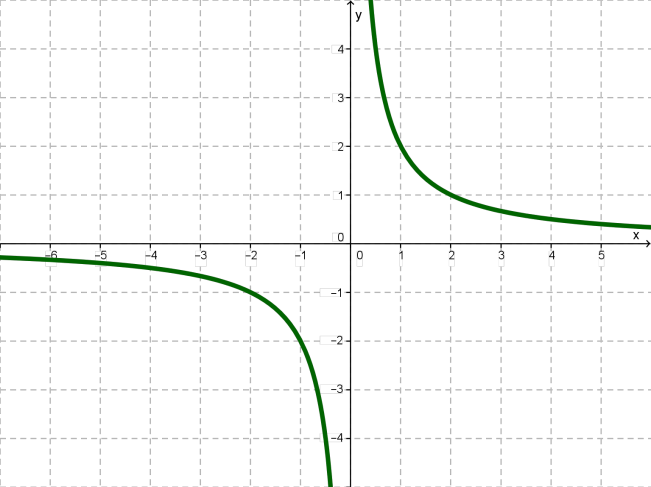
Հիմա դիտարկենք $k < 0$ դեպքերից որևէ մեկը, օրինակ՝ $k = - 1$ -ը:

Կառուցենք

y = - \frac{1}{x}

ֆունկցիայի գրաֆիկը (այստեղ $k = - 1$):

Ցանկացած $y = -f(x)$ ֆունկցիայի գրաֆիկը համաչափ է $y = f(x)$ ֆունկցիայի գրաֆիկին $x$-երի առանցքի նկատմամբ: Մասնավորապես,

y = - \frac{1}{x}

ֆունկցիայի գրաֆիկը համաչափ է

y = \frac{1}{x}

ֆունկցիայի գրաֆիկին $x$ -երի առանցքի նկատմամբ: Ստանում ենք հիպերբոլ, որի ճյուղերը գտնվում են երկրորդ և չորրորդ քառորդներում:

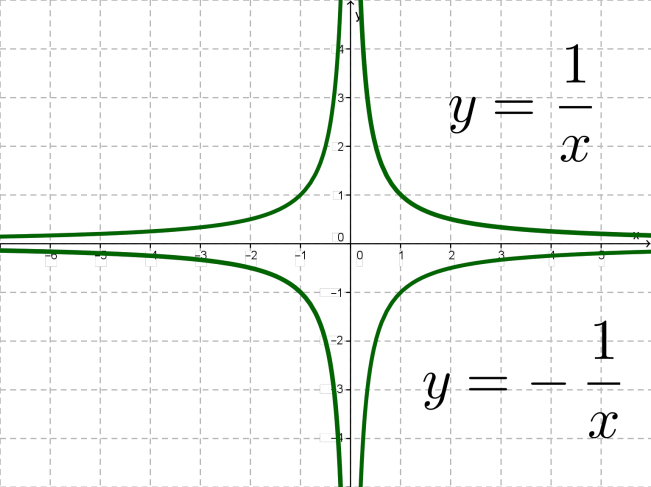
Ընդհանուր դեպքում՝

y = \frac{k}{x}

k \neq 0

ֆունկցիայի գրաֆիկը հիպերբոլ է:

1) Եթե $k > 0$, ապա նրա ճյուղերը գտնվում են առաջին և երրորդ քառորդներում:

2) Եթե $k < 0$, ապա նրա ճյուղերը գտնվում են երկրորդ և չորրորդ քառորդներում:

Հիշենք արդեն պարզած հատկությունները:

3) $(0; 0)$ կետը հիպերբոլի համաչափության կենտրոնն է:

4) $y = x$ և $y = -x$ ուղիղները հիպերբոլի համաչափության առանցքներն են:

5) $x$-երի և $y$-երի առանցքները հիպերբոլի ասիմպտոտներն են:

Սովորաբար ասում են, որ $x$ և $y$ մեծությունները հակադարձ համեմատական են, եթե $xy = k$ (որտեղ $k$ -ն $0$ -ից տարբեր թիվ է), կամ որ համարժեք է՝

y = \frac{k}{x}

Այս պատճառով

y = \frac{k}{x}

ֆունկցիան երբեմն անվանում են հակադարձ համեմատականության ֆունկցիա (ինչպես $y= kx$ -ը՝ ուղիղ համեմատականության ֆունկցիա):

$k$ թիվն անվանում են հակադարձ համեմատականության գործակից:

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Սխա՞լ ես գտել

\(x\)	\(1\)	\(2\)	\(-1\)	\(-2\)	\(4\)	$\frac{1}{2}$	\(-4\)	\(-\) $\frac{1}{2}$
\(y\)	\(2\)	\(1\)	\(-2\)	\(-1\)	$\frac{1}{2}$	\(4\)	\(-\) $\frac{1}{2}$	\(-4\)

2. y=k/x ֆունկցիայի գրաֆիկը